Transformer-Modelle wie GPT und BERT im Detail (German version)
Um die theoretische Grundlage zum Verständnis von Modellen wie GPT und BERT zu schaffen, umreiße ich in diesem Blogbeitrag einige Konzepte der Transformerarchitektur. Dazu diskutiere ich in 1 feedforward neuronale Netze. In Abschnitt 2 beschreibe ich rekurrente neuronale Netze mit einer Enkodierer-Dekodierer-Architektur und dem ersten Aufmerksamkeitsmechanismus. In 3 führe ich alle Elemente zusammen, um ein Transformer-Modell zu beschreiben. Abschließend gehe ich in 4 auf einige Aspekte der GPT-Modelle und BERTs ein.
Dieser Beitrag verfolgt zwei Ziele. Zum einen sollen Transformer-Modelle über ihre historische Genese erklärt werden, deshalb empfehle ich die Abschnitte 1 und 2 nachzuvollziehen, wobei das Augenmerk hier auf der Verarbeitung von Sequenzen mit einer Enkodierer-Dekodierer-Struktur liegen sollte. Zum anderen liegt den Transformer-Modellen ein ‘neuer’ (d.h. für das Jahr 2017 neuer) Selbstaufmerksamkeitsmechanismus zugrunde, bei welchem sich auch ein mathematisches Verständnis lohnt. Einmal mehr wird es hoffentlich für die Leserschaft nicht schwierig sein, diesen zu verstehen, sobald ein Gespür für vorangegangene Aufmerksamkeitsmechanismen da ist. Dieser Blogeintrag soll eine Hilfe sein, um Transformer-Modelle zu verstehen. Nichtsdestotrotz empfehle ich die zitierten Veröffentlichungen ebenfalls zu lesen. Eine chronologische Lektüre ist dazu sinnvoll.
1 Feedforward neuronale Netze
1.1 Definition eines neuronalen Netzes
Abstrakt betrachtet ist ein neuronales Netz zunächst ein Ansatz, um eine Funktion \(f(X; \theta)\) zu approximieren, durch die mit den Parametern \(\theta\) die Eingabewerte \(X\) abgebildet werden können (Goodfellow et al. 2016). Als Klassifikator würde ein Netz zum Beispiel mit den richtigen Parametern \(f(x)=y\) vorhersagen, wobei \(y\) einem Klassenlabel entspricht (Goodfellow et al. 2016).
Neuronale Netze bestehen aus einer Mehrzahl von verknüpften Funktionen, die mit Hilfe eines gerichteten kreisfreien Graphen eine Eingabe bis zur Ausgabe verarbeiten. Die jeweiligen Funktionen können auch als Schichten (layers) \(h_{i}\) mit \(i \in N\) und \(N\) als entsprechende Tiefe des Netzes bezeichnet werden. Die letzte Schicht wird als Ausgabeschicht \(a\) bezeichnet (siehe Fig. 1). Anstatt dass man jede Funktion einer Schicht nur als eine Abbildung eines Vektors auf einen Vektor betrachtet, sollte man die Funktionen eher als Kompositionen von Einheiten verstehen, die zusammen Vektoren auf Skalare abbilden, aus denen jeweils ein neuer Vektor geformt wird (Goodfellow et al. 2016).
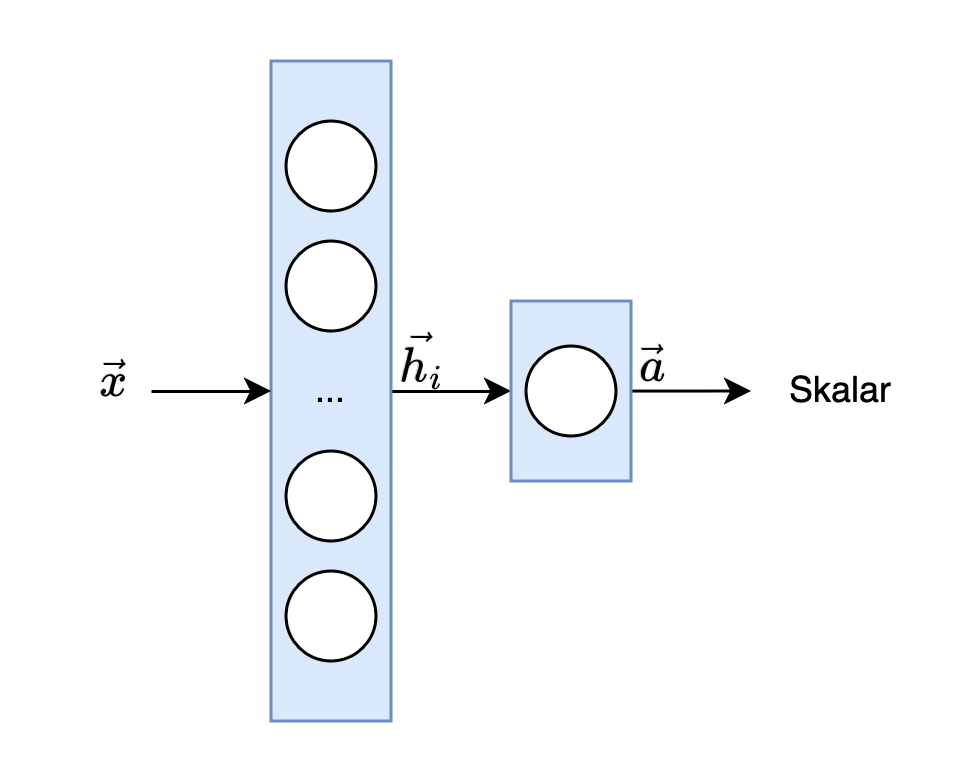
Fig. 1: Ein neuronales Netz mit Eingabe \(x\), Schicht \(h_i\), und Ausgabeschicht \(a\)
Das Konvolut an verknüpften Funktionen eines neuronalen Netztes umfasst auch nicht-lineare Funktionen (Aktivierungsfunktionen). Wir können die Schichten wie folgt definieren: \begin{equation} h_{linear} := W \cdot x + b \end{equation} \begin{equation} h_{nicht-linear} := \sigma(W \cdot x + b) \end{equation} wobei \(W\) eine Matrix mit Gewichten, \(x\) die Eingabe, \(b\) zusätzliche Biases, und \(\sigma\) eine Aktivierungsfunktion (z.B: Sigmoid, Tanh, Softmax) sind. Ein neuronales Netz wird als feedforward bezeichnet, wenn von der Eingabe bis zur Ausgabe des Informationsflusses keine Form von Feedback berücksichtigt wird (Goodfellow et al. 2016).
1.2 Training eines neuronalen Netzes
Die Approximation der Parameter \(\theta\) (damit sind die Gewichtungen und Biases des Netzes gemeint) folgt dem typischen Schema des maschinellen Lernens aus drei Schritten für jede Trainingsinstanz.
- Für \(x \in X\) sagt das Netz einen Wert \(y\) vorher.
- Dieser Wert wird mit einer weiteren Funktion, einer Verlustfunktion (oft auch als objective function bezeichnet), ‘bewertet’. Der Verlust gibt eine Information darüber ab, inwieweit sich die Vorhersage des Netzes von dem Soll-Wert unterscheidet (typische Verlustfunktionen sind z.B. Mean Squared Error oder Cross Entropy). Durch den Einbezug eines Zielwertes (manchmal auch als Ground Truth bezeichnet) kann hier auch vom überwachten Lernen gesprochen werden.
- Um zukünftige Verluste zu reduzieren, passt ein Optimierungsalgorithmus alle Parameter des Netzes auf der Grundlage der Verlustfunktion an. Ziel ist es, den Verlust durch Annäherung an sein globales (oder zumindest ein gutes lokales) Minimum zu minimieren. Der Einfluss der einzelnen Parameter auf den Verlust wird durch ihre Gradienten bestimmt. Diese können mit Hilfe der Kettenregel für das gesamte Netz berechnet wird. Auf der Grundlage der Gradienten können die Parameter des Modells so verändert werden, dass der Verlust bei nachfolgenden Vorhersagen verringert wird.
2 Rekurrente Netze mit einer Enkodierer-Dekodierer-Architektur
2.1 Definition eines rekurrenten neuronalen Netzes
Im Unterschied zu den feedforward Netzen werden bei rekurrenten neuronalen Netzen Informationen innerhalb einer Schicht mit den Zuständen \(h_{i}^{t}\) (auch hidden states bzw. verborgene Zustände genannt) ausgetauscht. Jeder Zustand zum Zeitpunkt \(t\) erhält nicht nur Informationen aus der Eingabe \(x\), sondern auch aus den vorangegangenen Eingaben, z.B. von \(x_{t-1}\), mit ihren jeweiligen Zuständen, also aus \(h_{i}^{t-1}\) usw. (vgl. Fig. 2).
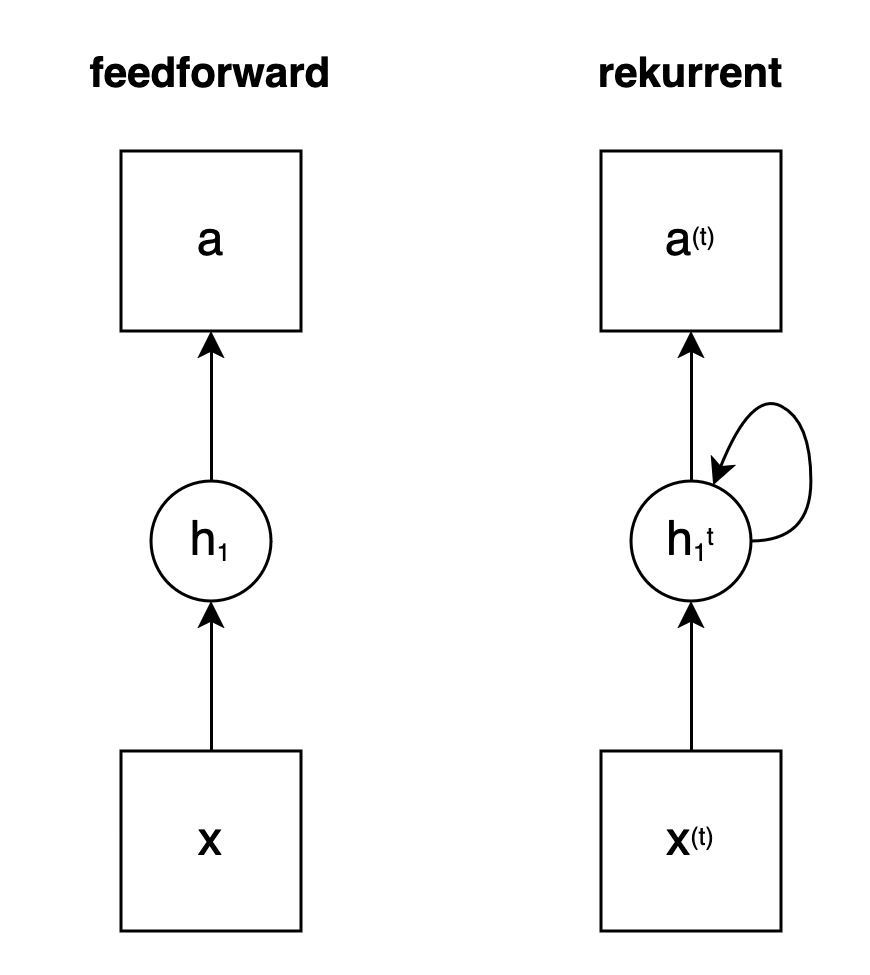
Fig. 2: Status eines neuronalen Netzes ohne (feedforward) und mit Feedback (rekurrent) sowie jeweils einer Eingabeschicht \(x\), einer verborgenen Schicht \(h_1\) und einer Ausgabe \(a\)
Der Vorteil rekurrenter neuronaler Netze wie dem Long Short-Term Memory-Modell (kurz LSTM in Hochreiter und Schmidhuber, 1997) liegt darin, insbesondere sequenzielle Daten wie zum Beispiel Sprache sehr gut modellieren zu können. Bei Sätzen sollte ein Netz die Vorhersage einer Eingabe auch von vorangegenangen Eingaben abhängig machen. Wie man mit Ferdinand de Saussure inspiriert pointieren kann: Die Bedeutung eines Wortes leitet sich aus dem Zusammenspiel der Differenzen der umliegenden Wörter ab (de Saussure, 1931). So kann auch ein neuronales Netz wenig Sinn aus einer isolierten Betrachtung eines jeden Wortes ableiten. Werden hingegen die Bedeutungen der umliegenden Worteingaben mit in einer Schicht eines rekurrenten Netzes einbezogen, das heißt insgesamt eine Sequenz, können dadurch komplexere Zusammenhänge abgebildet werden.
2.2 Ein auto-regressives Sprachmodell
Mit diesen Werkzeugen können wir bereits ein einfaches Sprachmodell zur Vorhersage von Sequenzen entwickeln. Angenommen wir wollen ein Modell, das eine Sequenz \(w\) mit \(w=(w_{1}, w_{2}, w_{3}, ..., w_{n})\) generiert, wobei \(n\) der Länge der Wörter entspricht, die zu der Sequenz, zum Beispiel einem Satz, gehören. Ein viel genutzter Ansatz in der natürlichen Sprachverarbeitung ist, die Vorhersage jedes Wortes durch alle vorangegangenen Wörter der Sequenz abzuleiten. Diese Idee können wir mit der Kettenregel für Wahrscheinlichkeiten wie folgt darstellen: \begin{equation} p(w) = p(w_{1}) \cdot p(w_{2}|w_{1}) \cdot p(w_{3}|w_{1}, w_{2}) \cdot … \cdot p(w_{n}|w_{1}, …, w_{n-1}) \end{equation} An dieser Stelle ist es bereits sinnvoll, nachzuvollziehen, dass wir hier eine auto-regressive Vorhersage der Sequenz verfolgen, bei der jedes Wort als abhängig von allen vorherigen Wörtern behandelt wird.
Auf das maschinelle Lernen anhand der Daten \(w\) übertragen folgt aus der vorgeschlagenen Sprachmodellierung, dass wir folgende Funktion approximieren wollen: \begin{equation} p(w; \theta) \end{equation} d.h. wir suchen die besten Parameter \(\theta\) mit vielen Sprachdaten (auch Korpora genannt) für unser Modell, mit denen wir eine Vorhersage für eine Sequenz von Wörtern \(w\) erreichen können, die den genutzten Daten entspricht. Die Approximation können wir durch ein Training sowohl mit einem einfachen feedforward neuronalen Netz als auch einem rekurrenten realisieren. Das rekurrente hat den Vorteil, dass es mit der Weiterreichung von zusätzlichen Informationen durch die Status innerhalb jeder seiner Schichten besser die vorangegangenen Wörter mit einbezieht.
2.3 Enkodierer-Dekodierer-Modelle zur maschinellen Übersetzung
Mit LSTM-Modellen entwickeln Sutskever et al. (2014) eine Sequenz-zu-Sequenz-Architektur zur maschinellen Übersetzung. Bei ihrem Ansatz kommen zwei wichtige Ideen zusammen. Zum einen (a) soll eine Übersetzung durch die Ursprungssprache bedingt werden, d.h. ein übersetzter Satz \(A\) (Ausgabe) hängt von seinem Ursprungssatz \(E\) (Eingabe) ab. Zum anderen (b) können Übersetzungen nicht immer wortwörtlich vollzogen werden. Aus diesem Grund ist es sinnvoll, dass ein Modell den ganzen Ursprungssatz berücksichtigt, bevor es eine potenzielle Übersetzung vorhersagt.
Die erste Idee (a) führt zu den bedingten Sprachmodellen: \begin{equation} p(w | c; \theta) \end{equation} Bei diesen Modellen hängt die Vorhersage der Wortsequenz nicht nur von jedem vorangegangen Wort ab, sondern wird auch durch den für die Übersetzung wichtigen Ursprungssatz \(c\) bedingt. Prinzipiell kann es sich aber auch um andere Informationen handeln, die so in die Vorhersage mit einfließen würden.
Die zweite Idee (b) setzen Sutskever et al. (2014) um, indem sie eine Architektur aus zwei Teilen, einem Enkodierer und einem Dekodierer (siehe Fig. 3), entwickeln (vgl. auch Cho et al. 2014). Wobei der Enkodierer den Ursprungssatz in eine feste Repräsentation \(c\) zusammenfasst und dann diese dem Dekodierer zum Vorhersagen der Übersetzung in der Zielsprache übergibt.
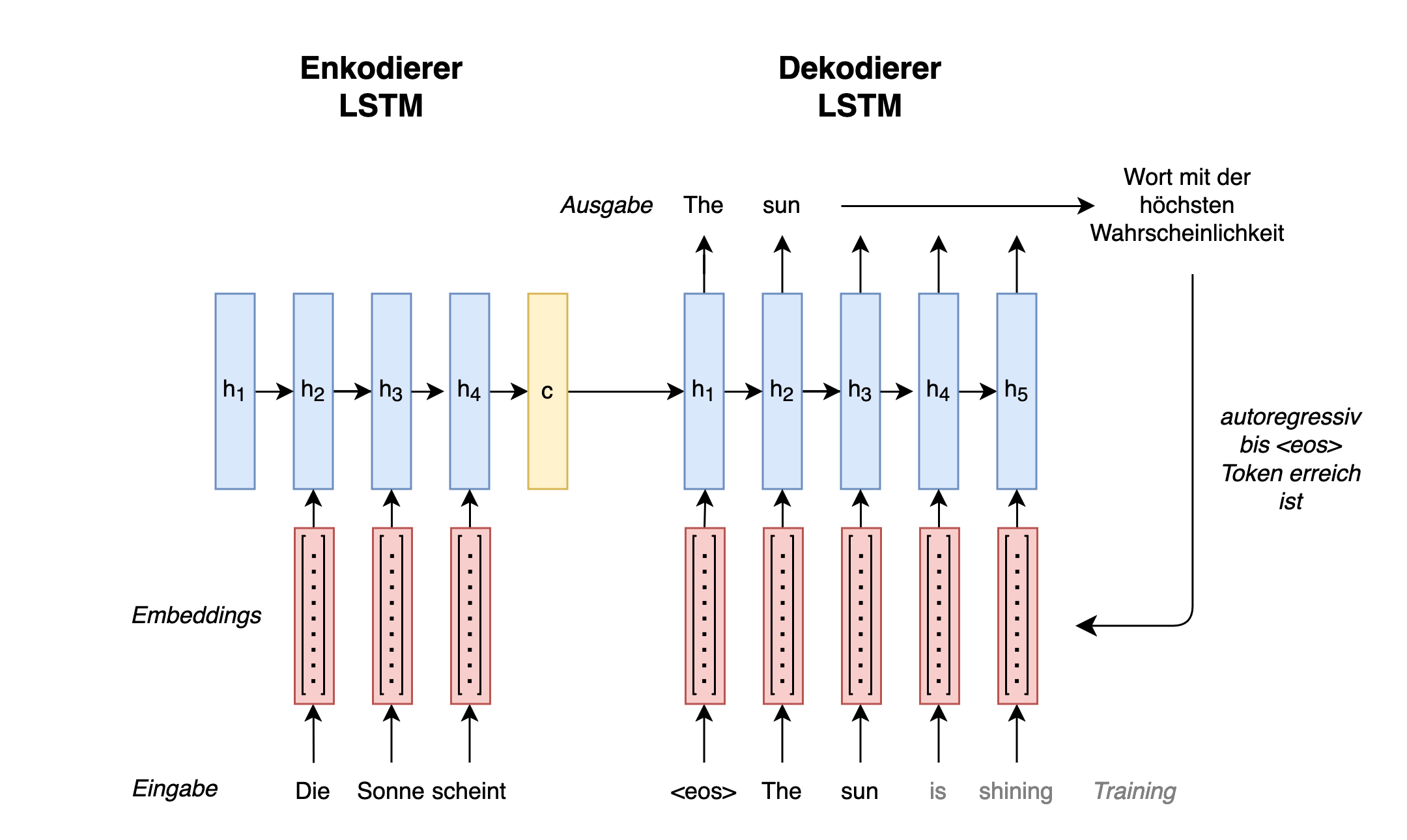
Fig. 3: Sequenz-zu-Sequenz-Architektur mit Enkodierer und Dekodierer
Für den Enkodierer nutzen Sutskever et al. (2014) ein LSTM-Modell, dem Vektorrepräsentationen (auch Embeddings genannt) für die Wörter einer Eingabesequenz aus der Ursprungssprache zugeführt werden. Es werden Embeddings aus dem einfachen Grund verwendet, da neuronale Netze nur mit Zahlen und nicht mit Buchstaben operieren können. Die verborgenen Status dieser Eingaben werden daraufhin durch das Modell zu einem finalen Zustand \(c\) zusammengeführt: \begin{equation} c = q({h^{1},…,h^{T}}) \end{equation} wobei \(q\) dem LSTM-Modell entspricht und \(T\) der Länge der Eingabesequenz. Der Zustand \(c\) wird dem Dekodierer übergeben.
Der Dekodierer besteht auch aus einem LSTM-Modell, welches auf der Grundlage des übergebenen Zustandes Wort für Wort eine Übersetzung in der Zielsprache vorhersagt. Dabei werden jedes übersetzte Wort und der Enkodierer-Endzustand der ursprünglichen Eingabe \(c\) regressiv dem Dekodierer so lange zugeführt, bis das Modell die Übersetzung abschließt: \begin{equation} p(w)= \prod_{t=1}^{T}p(w_{t}|{w_{1},…,w_{t-1}},c) \end{equation} Es schließt die Übersetzung ab, sobald es den Token <eos> vorhersagt. Mit diesem besonderen Token zeigen wir dem Modell bereits während des Trainings, an welcher Stelle Sequenzen beginnen und enden. In seinen Prädiktionen wird das Modell deshalb auch im besten Fall am Ende einer Sequenz noch diesen Token vorhersagen und den Inferenzprozess dadurch selbst terminieren.
Abschließend noch ein weiteres Wort zum Training eines Sequenz-zu-Sequenz-Modells: während des Trainings werden dem Enkodierer des Modells Sätze aus der Ursprungssprache und dessen Dekodierer deren Übersetzungen entsprechend eines Hyperparameters (z.B. mit Professor Forcing (Goyal et al., 2016)) gezeigt, wodurch die Gewichte \(\theta\) beider Kodierer stets zusammen gelernt und aufeinander abgestimmt werden können. Das Training eines solchen Modells wird wieder über eine Verlustfunktion wie Cross Entropy und einer Optimierung durch die Gradienten realisiert.
2.4 Der erste Aufmerksamkeitsmechanismus
Um die Qualität der Übersetzungen, insbesondere für lange Sequenzen, zu verbessern, führen Bahdanau et al. (2014) einen Aufmerksamkeitsmechanismus ein. Die Schwäche der Architektur nach Sutskever et al. (2014) liegt darin, dass die zu übersetzende Eingabe in eine einzige Repräsentation \(c\) gezwängt wird, mit welcher der Dekodierer eine Übersetzung finden muss. Allerdings spielen für eine Übersetzung nicht alle Wörter eines Satzes eine gleich große Rolle und auch kann die Beziehung unter den Wörtern variieren. Ob der Artikel in ‘the annoying man’ für ‘l’homme ennuyeux’ mit ‘le’ oder ‘l´’ übersetzt wird, hängt im Französischen beispielsweise davon ab, ob auf den Artikel ein Vokal folgt, gegebenenfalls mit einem stummen ‘h’ davor (Bahdanau et al. 2014). Bahdanau et al. (2014) entwickeln deshalb einen Mechanismus, der diesen Nuancen besser gerecht wird (vgl. Fig. 4).
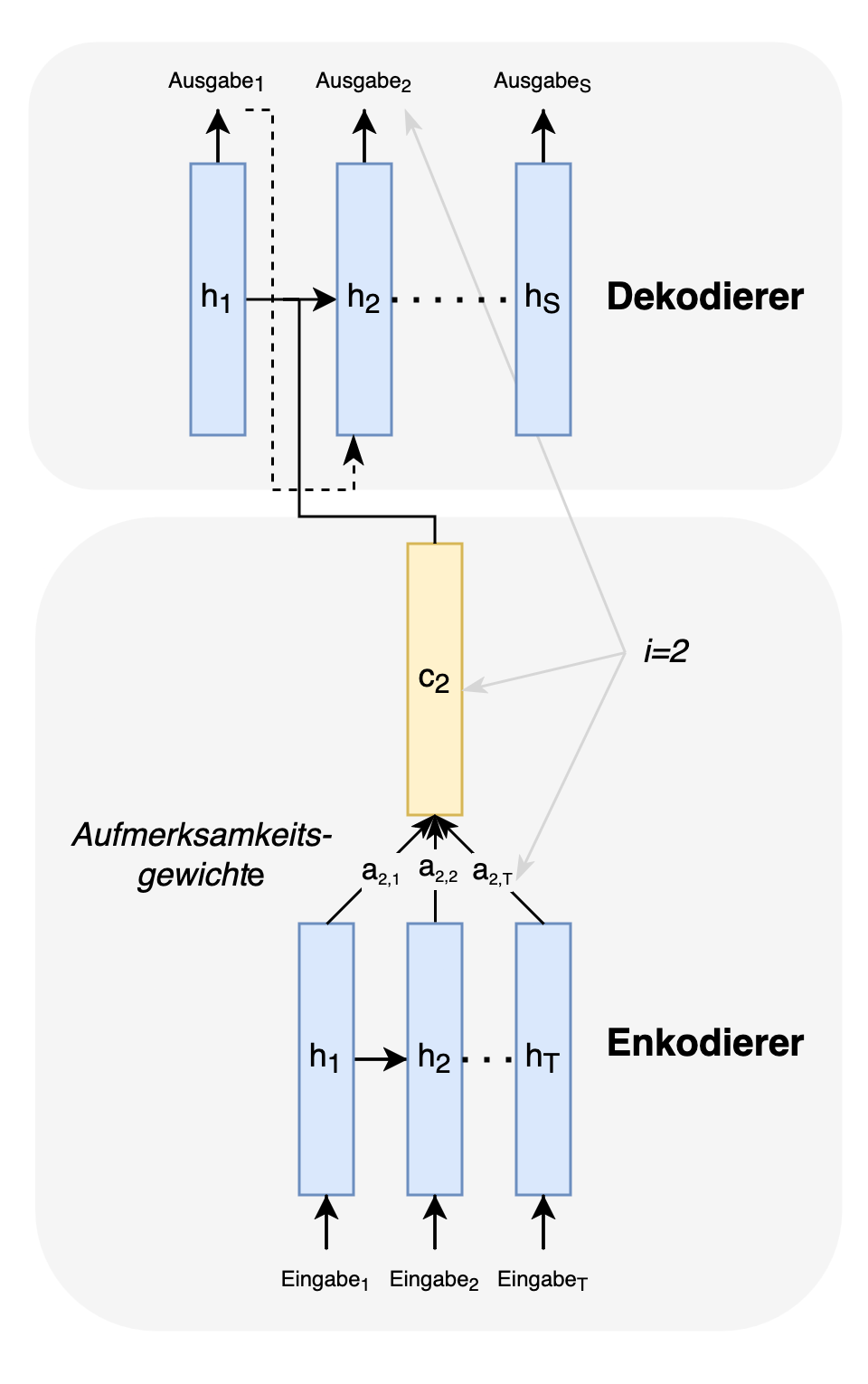
Fig. 4: Aufmerksamkeitsgewichte für eine Eingabe mit Bezug auf die Ausgabe an der Position i=2
Die um Aufmerksamkeit erweiterte Architektur übermittelt dem Dekodierer statt \(c\) für jede Eingabe kontextabhängige Zustände \(c_{i}\): \begin{equation} c_{i} = \sum_{t=1}^{T}a_{it}h^{t} \end{equation} Das Gewicht \(a_{it}\) für jeden Zustand \(h^{t}\) (in (Bahdanau et al. 2014) auch ‘Annotation’ genannt), wird wie folgt ermittelt: \begin{equation} a_{it} = \frac{\exp(e_{it})}{\sum_{k=1}^{T}\exp(e_{ik})} \end{equation} wobei \(a_{it}\) eine Normalisierung (Softmax-Funktion) für das Modell \(e_{it}\) ist. Dieses Modell ist wiederum ein Feedforward-Netz mit einer einzelnen Schicht, das bewertet, wie gut die Eingabe zum Zeitpunkt \(t\) mit der Ausgabe an Position \(i\) übereinstimmt. Damit erhält insgesamt jede Eingabe \(x^{1}...x^{T}\) eine eigene Menge an Aufmerksamkeitsgewichten, die in \(c_{i}\) resultieren, einem Kontextvektor, der dem Dekodierer hilft für jede Eingabe die passende Ausgabe (z.B. ‘l’homme’) zu bestimmen.
3 Transformer-Modelle mit Selbstaufmerksamkeit
3.1 Die Struktur eines Transformer-Modells
Die Transformerarchitektur (Vaswani et al., 2017) führt einige der zuvor genannten Elemente zusammen. Die Architektur verleiht dabei dem Aufmerksamkeitsmechanismus eine wesentlich größere Rolle und verzichtet auf rekurrente Strukturen.
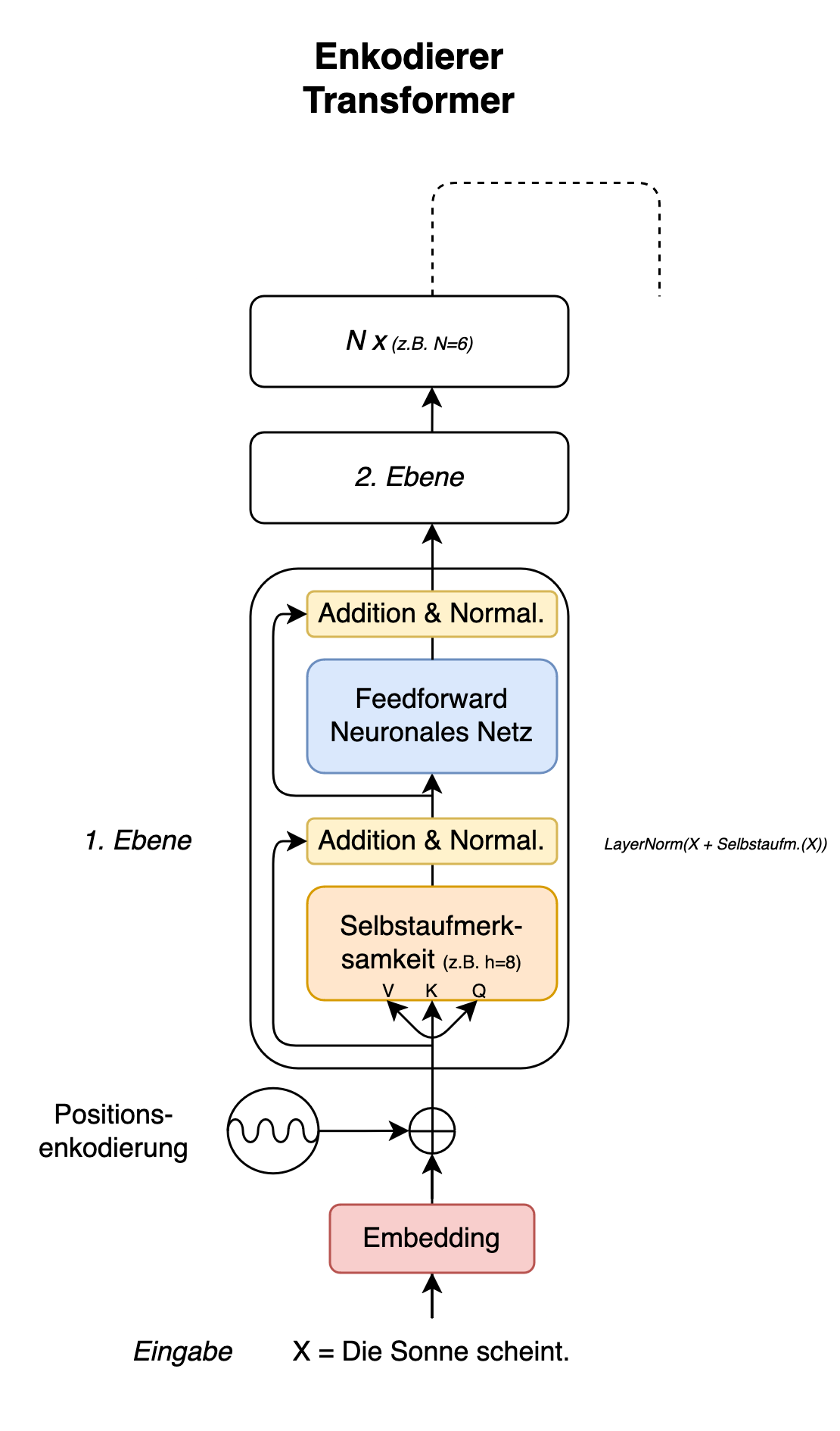
Fig. 5: Enkodierer eines Transformer-Modells
Der Enkodierer der Transformerarchitektur besteht aus Ebenen mit jeweils zwei Komponenten, durch die die eingehenden Informationen verarbeitet werden (vgl. Fig. 5). Eingaben werden als erstes einer Schicht mit einem Selbstaufmerksamkeitsmechanismus parallel zugeführt, der in Vaswani et al. (2017) vorgestellt wird. Nachdem dieser Mechanismus angewendet wurde, werden die Informationen normalisiert und daraufhin einer weiteren Schicht mit einem feedforward neuronalen Netz übergeben. Die Verarbeitung der Eingaben findet auf dieser Schicht wiederum einzeln statt. Für den Zwischenschritt der Normalisierung werden Mittelwerte und Standardabweichungen nach dem Prinzip der Layer Normalization berechnet (Ba et al. 2016; es gibt auch Root Square Layer Normalization von Zhang & Sennrich (2019), die z.B. in Llama 2 angewendet wurde). Zusätzlich wird die normalisierte Ausgabe mit der Ausgabe der vorangegangenen Schicht addiert. Dies wird auch als ‘Residual Connection’ bezeichnet und ist eine Methode, um dem Problem verschwindender Gradienten während der Backpropagation etwas entgegenzuwirken.
3.2 Embeddings mit positioneller Enkodierung
Wie bei den vorigen Sequenz-zu-Sequenz-Architekturen wird die Eingabe zuerst in Embeddings überführt. Die Embeddings werden aber zusätzlich mit einer Positionsenkodierung versehen, die über eine Frequenzdarstellung (Sinus- und Kosinusfunktionen) realisiert wird. Dies begründet sich wie folgt. Im Gegensatz zu den rekurrenten Ansätzen verarbeitet die Aufmerksamkeitsschicht eines Transformerkodierers eine Eingabesequenz auf einmal und zum Beispiel im Falle einer Übersetzung nicht Wort für Wort. Ohne eine zusätzliche Information zur Position einer jeden Eingabe innerhalb einer Sequenz würden den Kodierern die wichtige Information fehlen, wie die einzelnen Wörter aufeinander folgen.
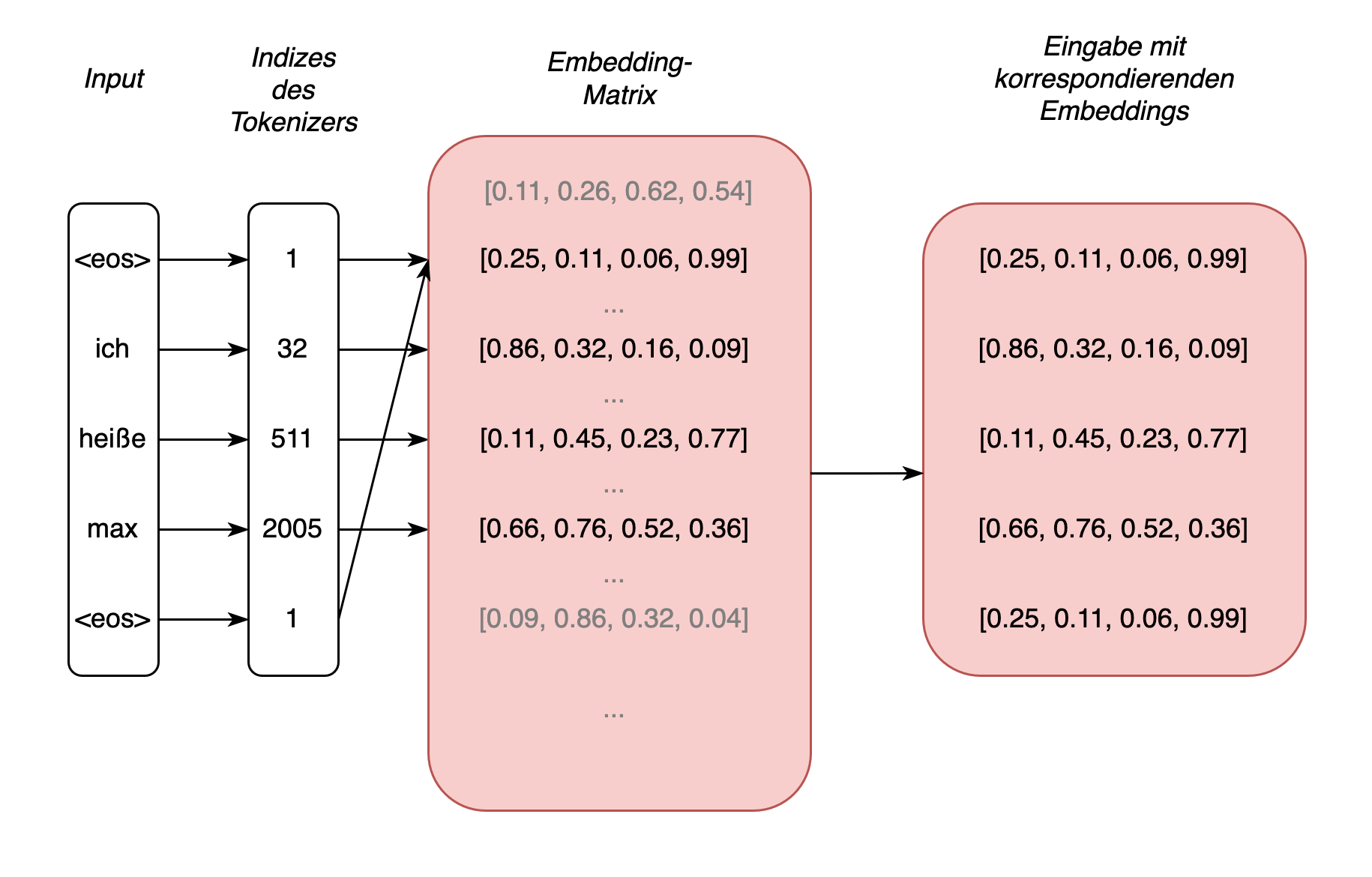
Fig. 6: Beispielsequenz, deren Tokens in Embeddings mit \(d=4\) überführt werden
Für die Verarbeitung der Eingabe hält die Transformerarchitektur eine Embedding-Matrix für alle Vokabeln der Daten bereit, die in das Training eines Tranformer-Modells einfließen. Die Größe der Matrix entspricht der Anzahl der Vokabeln (sonst als Tokens bezeichnet, zu denen auch bspw. Satzzeichen zählen) Kreuz einer gewählten Dimension (also n x d), mit der jedem Eingabetoken genau eine Zeile innerhalb der Matrix zugeordnet werden kann (vgl. Fig. 6). Die Anzahl der Spalten entspricht der gewählten Dimension. Die Matrixwerte für die Tokentypen werden während der Initialisierung eines Transformer-Modells zufällig ausgewählt. Es sind die Zeilen dieser Matrix, die auch als Embeddings bezeichnet werden. Man kann auch sagen, dass jeder Tokentyp eine Vektorrepräsentation besitzt. Wobei diese Vektoren in einem weiteren Schritt mit der positionalen Enkodierung addiert so der Eingabe eine einzigartige Darstellung verleihen. Entscheidend ist, dass die Embeddings der Transformerarchitektur sich im Laufe eines Trainings auch verändern, d.h. entsprechend der Daten angepasst, also ‘gelernt’ werden können. (Anmerkung 1: der erste Schritt ist, die Eingabetokens in eine Indexdarstellung zu überführen, mit der jedem Token eine Zeile in der Embedding-Matrix zugeordnet werden kann; Anmerkung 2 – es hat mich einige Zeit gekostet, das zu verstehen: BERT-Embeddings und dergleichen sind nicht die Embeddings aus der Eingabe; diese Embeddings sind vielmehr das Resultat aus der Verarbeitung der Aufmerksamkeitsmechanismen, und werden am Ende einer Transformer-Schicht entnommen.)
Zur Veranschaulichung der Positionsenkodierung ist es hilfreich, zunächst ein stark vereinfachtes Beispiel zu betrachten. Angenommen man teilt jedem Embedding einfach die Positionen (pos) des jeweiligen Tokens in Form von ganzen Zahlen mit \(n \in N\), wobei \(N\) der Länge der Eingabetokens inklusive <eos>-Token entspricht, zu. Wenn wir den Token “heiße” und dessen Embedding [0.11, 0.45, 0.23, 0.77] (ausgedachte Werte) auswählen, dann ließe sich für den Token innerhalb der Sequenz “<eos> ich heiße max <eos>” auf diese Weise eine Positionsenkodierung von [2, 2, 2, 2] ermitteln. Der Vektor hätte diese Werte, weil wir die zweite Position der Sequenz (Sequenz beginnt bei 0) und eine Embedding-Dimension von \(d=4\) ausgewählt haben. Der Transformer-Architektur entsprechend könnten wir diesen Vektor anschließend auf das Embedding des Tokens addieren [2.11, 2.45, 2.23, 2.77] und hätten diesem auf diese Weise zusätzliche Informationen hinzugefügt. Dieser Ansatz würde jedoch zu mehreren Problemen führen. Zu nennen sind hier beispielsweise große Werte für lange Sequenzen, deren Positionsenkodierung die Werte der Embeddings stark beeinflussen würden, und es würde ein relativer Bezug wiederkehrender Positionsmuster fehlen.
Vaswani et al. (2017, S. 6) stellen deshalb eine Positionsenkodierung vor, durch die jedem Token-Embedding über das Bogenmaß der trigonometrischen Funktionen zusätzliche Informationen zu der Position des Tokens innerhalb einer Sequenz zugeführt werden. Die Vorteile dieses Ansatzes sind unter anderem, dass die Positionsenkodierungswerte auf ein Intervall von \([-1,1]\) beschränkt werden können, und die Periodizität der trigonometrischen Funktionen auch erlaubt, wiederkehrende Muster abzubilden. Denn bestimmte Abstände zwischen Positionen werden ähnliche Werte erzeugen. Dadurch kann das Modell leichter lernen, dass sich bestimmte Muster oder Abstände zwischen Tokens in unterschiedlichen Bereichen einer Sequenz wiederholen, unabhängig von der genauen Position in der Sequenz.
Die Positionen der Tokens werden nach Vaswani et al. (2017) wie folgt berechnet: \begin{equation} PE_{(pos, 2i)} = sin(\frac{pos}{10000^{\frac{2i}{d}}}) \end{equation} \begin{equation} PE_{(pos, 2i+1)} = cos(\frac{pos}{10000^{\frac{2i}{d}}}) \end{equation} pos entspricht der absoluten Position innerhalb einer Eingabesequenz der Länge N, der Wert \(10000\) ist eine gewählte Konstante, und i verweist auf die Indezes der Embeddings. Zum Beispiel bei einer gewählten Dimension der Embedding-Vektoren mit \(d=4\) gilt \(i \in I= \{0, 1, 2, 3\}\). Schließlich erlauben die beiden Sinus- und Kosinusfunktionen für gerade und ungerade Indizes unterschiedliche Werte zu ermitteln. Für alle gerade Indizes eines Embeddings können wir (10) und für alle ungeraden (11) verwenden. Erwähnenswert ist hier, dass die Frequenzen der Sinus- und Kosinusfunktionen der PE von der gewählten Dimension abhängig sind. Kleine Embedding-Dimensionen führen zu höheren Frequenzen (feinere Positionsauflösungen) und hohe Dimensionen zu niedrigeren Frequenzen (gröbere Positionsauflösungen). Anhand dieser Vorgaben wird schließlich für jede Eingabe eine Positionsenkodierungs-Matrix berechnet – also für jeden Token ein Positionsvektor (vgl. Fig. 7) – welche wir daraufhin auf die Token-Embeddings addieren können. Im Zusammenspiel mit den Embeddings wird dem Transformer-Modell dadurch eine kontextsensitive Repräsentation der Tokens zur weiteren Verarbeitung überreicht.
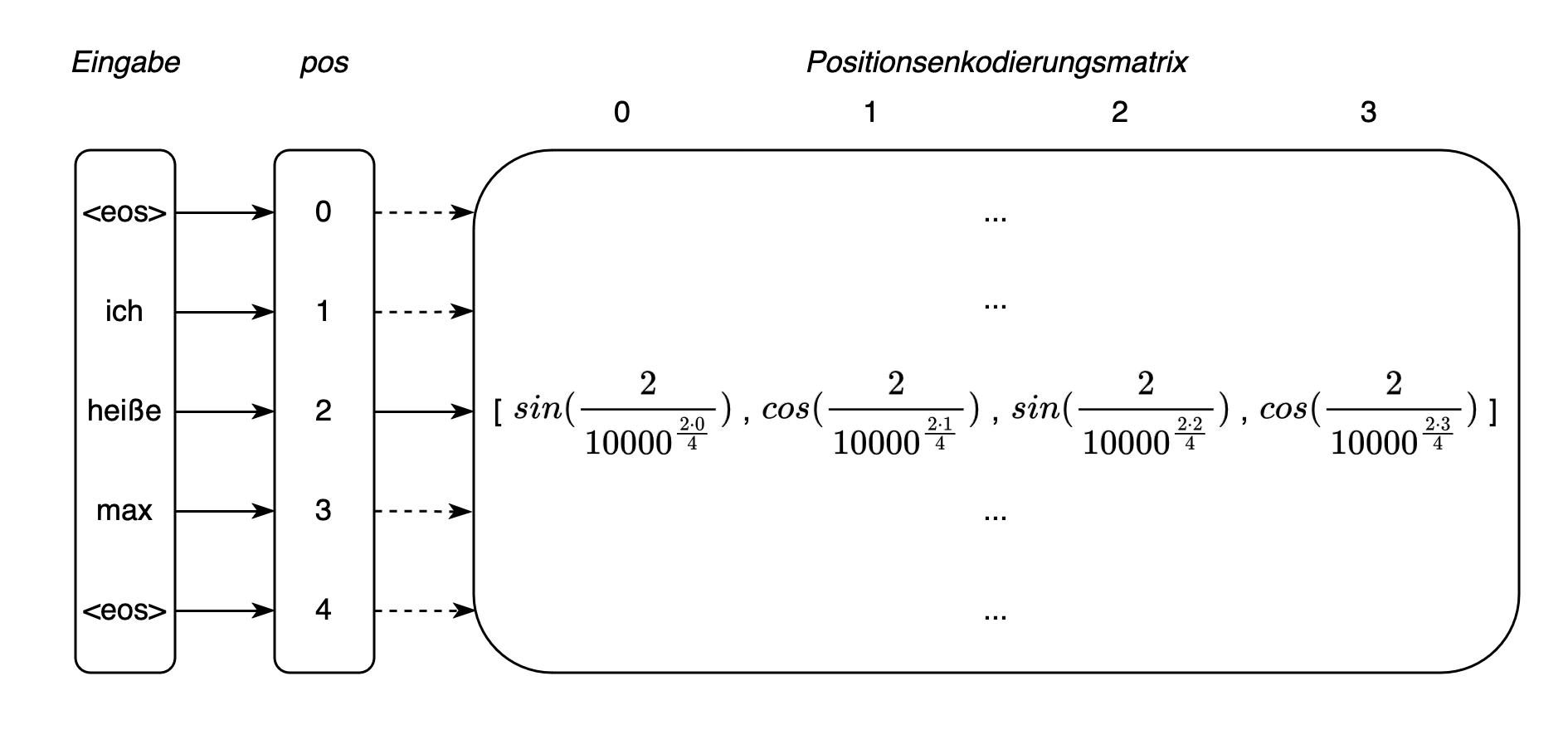
Fig. 7: Beispielsequenz, deren Tokens in Positionsenkodierungen mit \(d=4\) überführt werden
3.3 Selbstaufmerksamkeitsmechanismus
Im Gegensatz zu dem Aufmerksamkeitsmechanismus nach Bahdanau et al. (2014) entwickeln Vaswani et al. (2017) einen Selbstaufmerksamkeitsmechanismus, den sie auch als ‘skalierte Skalarprodukt-Aufmerksamkeit’ beschreiben (Vaswani et al., 2017, S.3). Die für Transformer genutzte Selbstaufmerksamkeit kann vereinfacht zunächst mit der Operation aus (8) verglichen werden (Raschka et al., 2022). Wir können für einen kontextsensitiven Vektor \(z_{i}\) einer Eingabe an der Stelle \(i\) die Aufmerksamkeit wie folgt berechnen (Raschka et al., 2022): \begin{equation} z_{i} = \sum_{j=1}^{T}a_{ij}x^{j} \end{equation} wobei \(a_{ij}\) nicht mit einem Status \(h^{t}\), sondern mit den Eingaben \(x^{j}\) multipliziert wird, mit \(j\in{\{1, ..., T\}}\) einer Eingabesequenz der Länge \(T\) (vgl. die Summe über alle \(x^{j}\) in (12)). Im Unterschied zu Bahdanau et al. (2014) ist \(a\) dabei keine Normalisierung von einfachen feedforward Netzen \(e_{ij}\), sondern eine Softmax-Normalisierung über die Skalarprodukte \(\Omega\) der Eingabe \(x^{i}\) bezogen auf alle anderen Eingaben \(X=x^{1}, ..., x^{T}\) (Raschka et al., 2022): \begin{equation} a_{ij} = \frac{\exp(\omega_{ij})}{\sum_{j=1}^{T}\exp(\omega_{ij})} \end{equation} mit (Raschka et al., 2022): \begin{equation} \omega_{ij} = x^{(i)T}x^{j} \end{equation} Was wir hier gleichzeitig im Unterschied zum Aufmerksamkeitsmechanismus von Bahdanau et al. (2014) sehen, bei welchem die Aufmerksamkeit insbesondere die Ausgabe des Dekodierers (dort an Ausgabeposition i) mit einbezieht, ist, dass das Aufmerksamkeitsgewicht in (13) mit (14) sich auf die anderen Eingaben einer Sequenz bezieht. Eben aus diesem Grund ist es sinnvoll, von einer Selbstaufmerksamkeit zu sprechen.
Zu dieser Darstellung der Aufmerksamkeit fügen Vaswani et al. (2017) eine weitere Veränderung für jede Eingabe \(x^{i}\) hinzu, und zwar wird das Gewicht \(a\) nicht mit \(x^{j}\) multipliziert, sondern mit einem Wert \(v^{j}\): \begin{equation} z_{i} = \sum_{j=1}^{T}a_{ij}v^{j} \end{equation} Denn Vaswani et al. (2017) überführen jedes \(x^{i}\) in ein Tripel aus (\(v^{i}\), \(k^{i}\), \(q^{i}\)) mittels den Projektionsmatrizen (\(W_{v}\), \(W_{k}\), \(W_{q}\) – die hier auch als zusätzliche lineare Schichten aufgefasst werden können). Die Idee dahinter entstammt dem Information Retrieval, das mit Wert-, Schlüssel-, Abfragetripeln arbeitet (wegen Values, Keys, Queries die Abkürzungen v, k, q). Die V, K, Q in Fig. 5 und Fig. 8 entsprechen: \(V=XW_{v}\), \(K=XW_{k}\) sowie \(Q=XW_{q}\) (vgl. Fig. 9). Die Skalarprodukte des Selbstaufmerksamkeitsmechanismus für jede Eingabe werden in Vaswani et al. (2017) auch nicht mit (14) berechnet, sondern mit den Abfrage- und Schlüsselwerten (Raschka et al., 2022): \begin{equation} \omega_{ij} = q^{(i)T}k^{j} \end{equation} Die Aufmerksamkeitsgewichte werden abschließend mit der Dimension der Embeddings noch skaliert (\(\frac{\omega_{ij}}{\sqrt{d}}\)). Die zusätzliche Skalierung begründen Vaswani et al. (2017, S. 4) mit der Beobachtung, dass zu große Werte der Skalarprodukte (vgl. (14)) die für die zusätzliche Normalisierung genutzte Softmax-Funktion in einen Bereich führen, der beim Lernen in sehr kleine Gradienten resultiert.
Kurz: Neben der Aufmerksamkeit einer Eingabe \(x^i\) gegenüber allen anderen Eingaben innerhalb einer Sequenz \(X\) wird die Selbstaufmerksamkeit noch durch verschiedene Darstellungen aller \(x^j \in X\) in Form der Abfrage-, Schlüssel-, Wertrepräsentationen berechnet. Die Selbstaufmerksamkeit kann auch als Scoring-Mechanismus beschrieben werden, der die Relevanz von benachbarten Token für jeden Token bestimmt (siehe Fig. 8:).
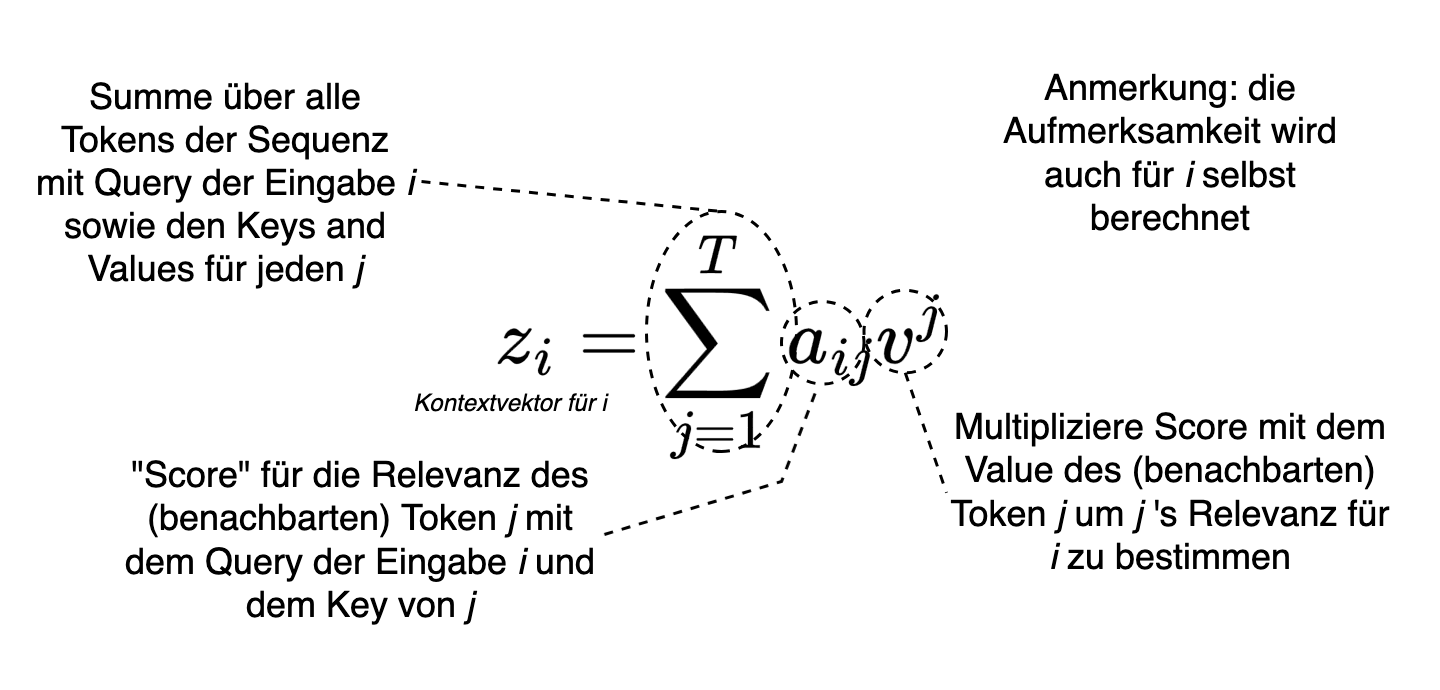
Fig. 8: Aufmerksamkeitsmechanismus als Score zur Bestimmung der Relevanz von Token aus dem Kontext
Die Aufmerksamkeit kann \(h\)-Mal parallel berechnet, wobei \(h\) einer gewählten Anzahl an Köpfen (auch Attention Heads gennant) entspricht. Vaswani et al. (2017) wählen \(h=8\) Köpfe, deren Werte konkateniert abschließend der Layer-Normalisierung in den Kodierern weitergereicht werden (siehe Fig. 9 und Fig. 5). Die Verwendung mehrerer Köpfe wird als ‘Multi-head Attention’ bezeichnet.
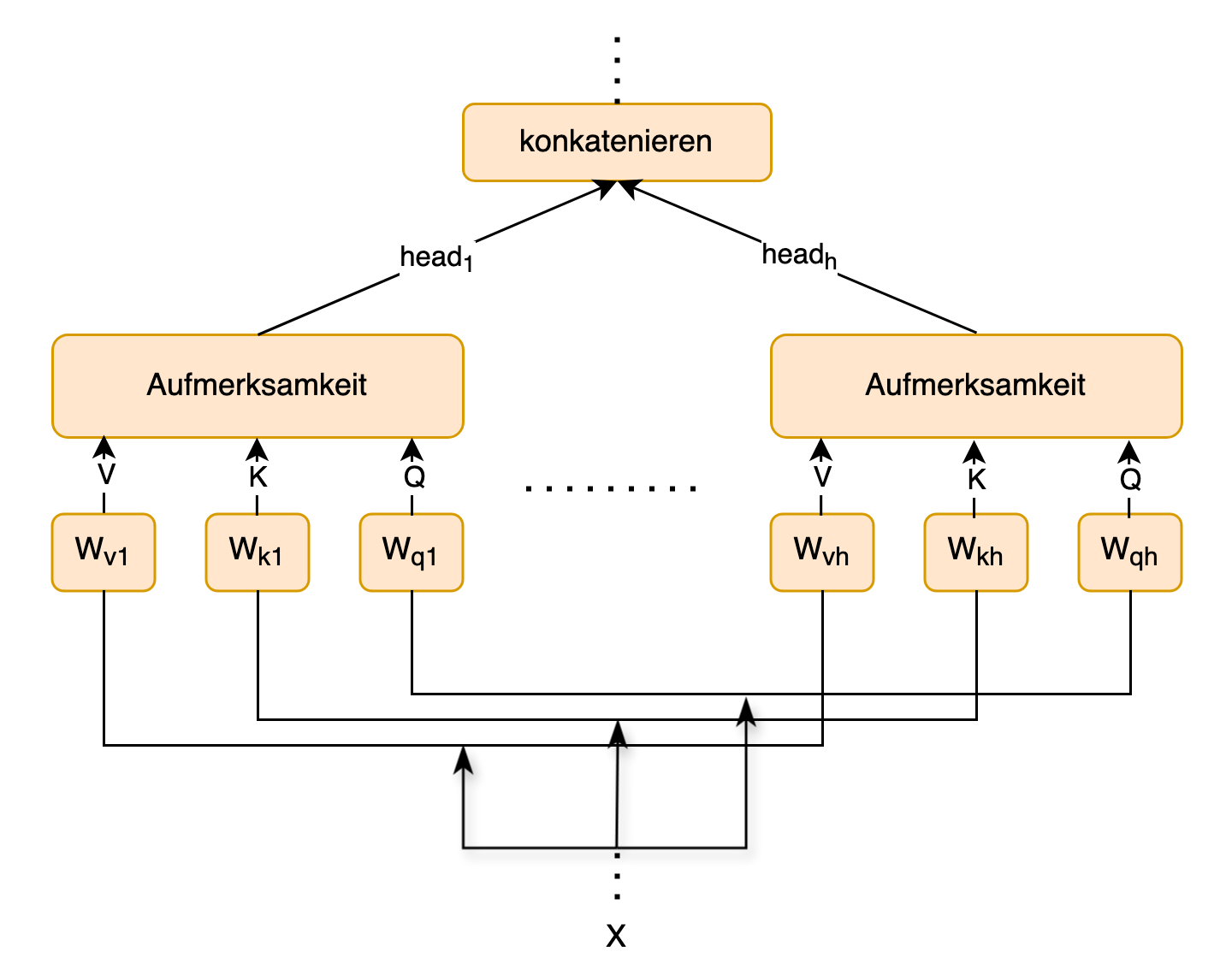
Fig. 9: Aufmerksamkeit für eine Eingabe X mit mehreren Köpfen (heads)
3.4 Der Transformer-Dekodierer
Der Dekodierer der Transformerarchitektur folgt strukturell dem Enkodierer. Er enthält jedoch noch eine zusätzliche Schicht (vgl. Fig. 10). In dieser Schicht werden die ausgegebenen Informationen des Enkodierers (z.B. der enkodierte Ursprungssatz einer Übersetzung) über die Wert- und Schlüsselwerte \(V\), \(K\) mitberücksichtigt. Die Abfragewerte \(Q\) kommen hingegen von der vorangegangenen Aufmerksamkeitsschicht des Dekodierers. Durch die Kombination der Informationen sowohl des Enkodierers als auch des Dekodierers wird diese weitere Schicht auch als ‘Cross-Aufmerksamkeitsschicht’ bezeichnet. Da dabei Enkodierer-Informationen mit einbezogen werden, lässt sich bei dem ganzen Modell (Enkodierer + Dekodierer) zudem von einem bedingten Sprachmodell sprechen, wie dieses zuvor in (5) vorgestellt.
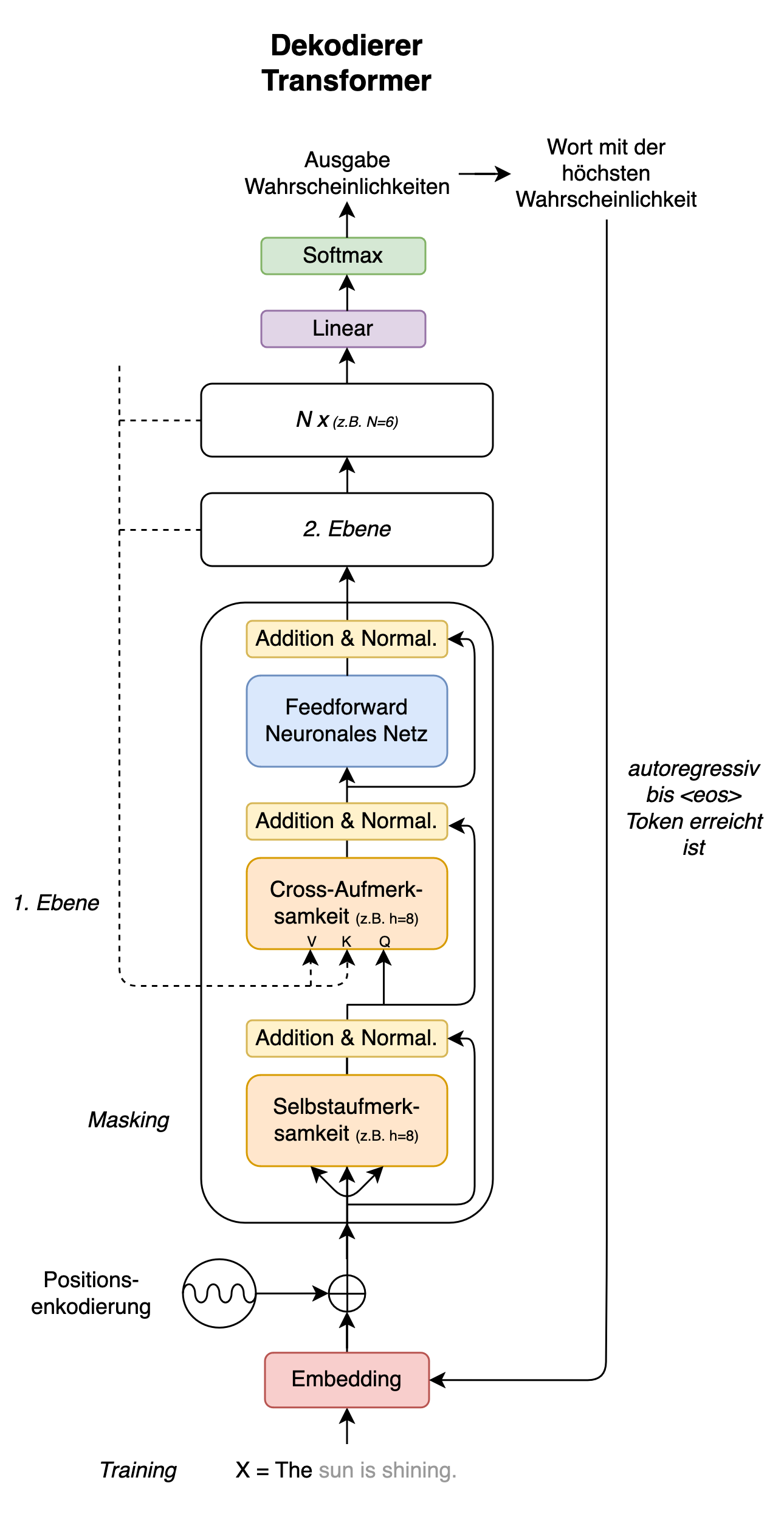
Fig. 10: Dekodierer eines Transformer-Modells
Die Selbstaufmerksamkeitsschicht des Dekodierers erlaubt es, Teile der Dekodierereingabe zu verdecken (dies wird auch als Masking beschrieben, geanuer gesagt Causal Masking). Ein Transformer-Enkodierer lässt hingegen grundsätzlich eine Betrachtung aller Eingaben gleichzeitig zu. Das Masking spielt eine wichtige Rolle bei dem Ziel des Dekodierers: z.B. die Vorhersage einer Übersetzung. Zur Prädiktion einer Übersetzungssequenz arbeitet der Dekodierer sich jeweils autoregressiv von Token zu Token vor (z.B. von links nach rechts, vgl. hierzu auch (7)). Das bedeutet, dass beim Inferenzieren jede Prädiktion nur mit Hilfe vorangegangener Tokens arbeitet, die anderen bleiben im übertragenen Sinne maskiert. Für das Training können dem Modell noch durch Professor Forcing korrekte Übersetzungen als Eingabe mit zugeführt werden, um eine Fehlerfortpflanzung zu minimieren – wie bei den zuvor beschriebenen Sequenz-zu-Sequenz-Modellen. Grundsätzlich ist das Trainingsziel die Vorhersagen des Modells anhand der Übersetzungslösungen zu optimieren. Ein Übersetzungsprozess terminiert in jedem Fall, wenn der Token <eos> oder die zuvor definierte maximale Sequenzlänge erreicht sind.
Abschließend noch ein Wort zu der linearen Schicht am Endes des Dekodierers (vgl. Fig. 10). Die unmittelbare Ausgabe aus den Aufmerksamkeitsblöcken umfasst eine durch das Modell angereicherte Repräsentation der Eingabe-Embeddings \(h_{i}\). In diese Repräsentation sind durch die Aufmerksamkeitsmechanismen und den feedforward-neuronalen Netzen zusätzliche Informationen umliegender Tokens sowie des Enkodierers mit eingeflossen. Es gilt jedes \(h_{i}\) wieder in eine Darstellung des Vokabulars zu überführen. Dafür stellt die lineare Schicht eine Projektionsmatrix \(W\) bereit. Diese ähnelt einer Schicht eines neuronalen Netztes mit dem Unterschied, dass hier keine nicht-lineare Aktivierungsfunktion den Informationsfluss noch weiter verändert.
Betrachten wir dazu ein Beispiel. Angenommen dem Modell liegt eine Vokabelgröße von \(10 000\) zugrunde und für die Embeddings bzw. die Status des Modells wählen wir exemplarisch eine Dimension von \(d=512\). Dann können wir mit \(W\) (10000 x 512) alle \(h_{i}\) in einen Logits-Vektor überführen, der der Dimension des Vokabulars entspricht, und dessen Wert gleichzeitig die Approximation des Modells dafür ist, wie wahrscheinlich welcher der Token des Vokabulars ist: \begin{equation} logits = W \cdot h_{i} + b \end{equation} wobei \(b\) als zusätzlicher Bias auf noch einen Einfluss auf die Abbildung nimmt. Auf der Grundlage dieses Logits-Vektor (z.B. \(logits = [3.4, -1.2, 0.5, ..., 2.7]\)) kann schlussendlich die Softmax-Aktivierung, mit der die Werte des Vektors in Wahrscheinlichkeiten überführt werden, den wahrscheinlichsten Token für den ausgegebenen Status \(h_{i}\) des Dekodierers vorhersagen. An dieser Stelle ließen sich aber auch andere Dekodierungsstrategien (z.B. Beam-Search oder Greedy Decoding) einsetzen.
Insgesamt unterscheiden sich Inferenz und Training bei einem Transformer-Modell nicht von anderen neuronalen Netzen (siehe Kapitel 1.2).
4 GPT, BERT und co
Derweil die ursprüngliche Transformerarchitektur zur maschinellen Übersetzung entwickelt wurde, haben sich Transformer-Modelle bei anderen Aufgaben ebenfalls bewährt. Am bekanntesten sind große Sprachmodelle wie Generative Pre-trained Transformer-Modelle (Radford et al., 2018) von OpenAI, die eine Eingabe (Prompt) mit einem Transformer-Dekodierer sozusagen ‘weiterschreiben’, d.h. die nächsten Tokens der Sequenz vorhersagen. Sprachmodelle wie GPT bestehen dabei nur aus Dekodierer-Ebenen. Das Bidirectional Encoder Representations from Transformers-Modell (kurz BERT, Devlin et al., 2019) ist wiederum ein reiner Transformer-Enkodierer. Das heißt mit BERT können keine neuen Wörter oder Sätze in einer Zielsprache autoregressiv generiert werden. BERT stellt dafür Enkodierungen bereit, mit deren Hilfe sich zum Beispiel Klassifikationsaufgaben lösen lassen. Grundsätzlich besteht die Entwicklung der meisten Transformer-Modelle aus zwei Phasen: einem Vortraining und einem Feintuning für gezielte Anwendungen. Zum Schluss stelle ich diese beiden Schritte anhand von BERT vor.
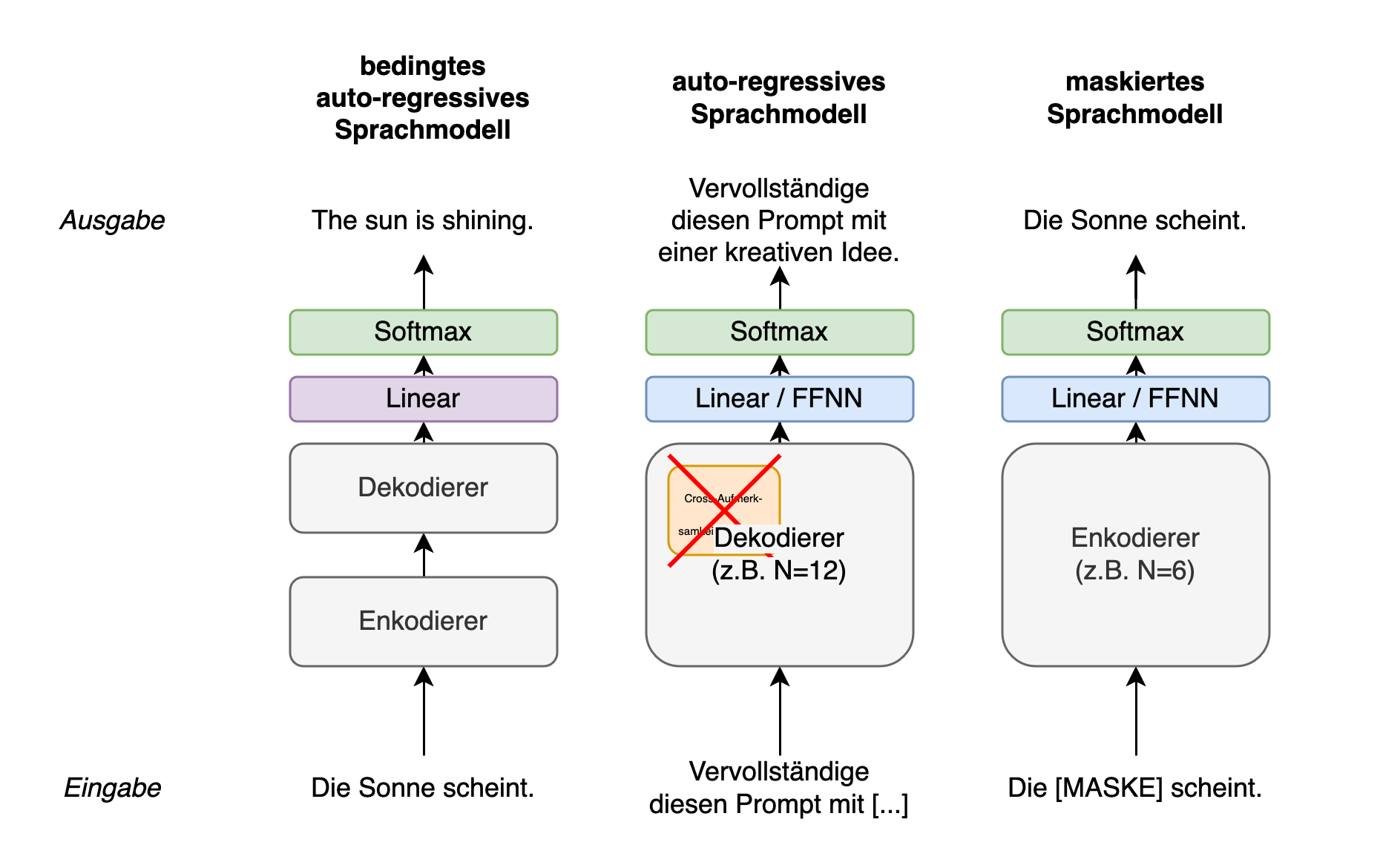
Fig. 11: Verschiedene Transformerarchitekturen: Enkodierer-Dekodierer zur maschinellen Übersetzung (auch MTM genannt), einzelne Dekodierer zur Generierung von Sequenzen (auch als LM bezeichnet), und einzelne Enkodierer für Downstream-Aufgaben (auch häufig als MLM bezeichnet)
4.1 Das Bidirectional Encoder Representations from Transformers-Modell
Für BERT trainieren Devlin et al. (2019) zunächst den Enkodierer eines Transformer-Modells vor dem Hintergrund zweier Aufgaben. Die erste Aufgabe des BERT-Trainings besteht aus einer maskierten Sprachmodellierung (Masked Language Modelling). Das Modell bekommt dabei Sätze gezeigt, bei denen es 15% zufällig ausgewählte Wörter, die verdeckt werden, vorhersagen muss. Die zweite Aufgabe besteht aus einer binären Klassifikation zweier Sätze, und zwar mit dem Ziel, vorherzusagen, ob diese aufeinander folgen oder nicht. Wobei das Modell 50% korrekte Satzfolgen und 50% inkorrekte Folgen gezeigt bekommt. Da das Modell ausschließlich einen Enkodierer verwendet – und keine ‘rechtsbündige’ Maskierung der jeweils nächsten Tokens innerhalb einer Sequenz wie bei einem Transformer-Dekodierer vorgenommen wird – kann das Training auch als bi-direktional bezeichnet werden. Der Enkodierer hat Zugang zu jeder Eingabe von beiden Seiten. Devlin et al. (2019) bezeichnen das Training ihres Enkodierers auf den beiden Aufgaben als Vortraining.
In einem weiteren Schritt nutzen Devlin et al. (2019) das vortrainiertes BERT-Modell für weitere Experimente aus der natürlichen Sprachverarbeitung. Dafür feintunen sie BERT beispielsweise, um die plausibelste Wortfolge für Sätze aus dem Datensatz Situations With Adversarial Generations (Zellers et al., 2018) zu klassifizieren. Dazu bekommt BERT für das Training verschiedene mögliche Fortsetzungen gezeigt. Aus diesen muss das Modell die plausibelste auswählen. Da BERT ursprünglich vor dem Hintergrund anderer Aufgaben vortrainiert wurde, die Gewichte des Modells jedoch auch für solche neue Aufgaben verwendet und angepasst werden können, kann ein solches Feintuning BERTs auch als eine Form des Transferlernens bezeichnet werden.
Zusätzliche Ressourcen
- Ich kann Brendan Bycrofts Visualisierung von Transformer-Modellen empfehlen: https://bbycroft.net/llm
- Mit die besten Erklärungen und Visualisierungen zu verschiedenen Modellierungsansätzen in NLP, einschließlich der Transformer-Architektur, stellt Lena Voita bereit: https://lena-voita.github.io/nlp_course.html
- Weitere hilfreiche Visualisierungen zu BERT gibt Jay Alammar: https://jalammar.github.io/illustrated-bert/
Bibliographie
Ba, J., Kiros, J.R., & Hinton, G.E. (2016). Layer Normalization. ArXiv, abs/1607.06450.
Bahdanau, D., Cho, K., und Bengio, Y. (2014). Neural Machine Translation by Jointly Learning to Align and Translate. CoRR, abs/1409.0473.
Cho, K., van Merri ̈enboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., und Bengio, Y. (2014). Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation. In Moschitti, A., Pang, B., und Daelemans, W., Herausgeber, Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Seiten 1724–1734, Doha, Qatar. Association for Computational Linguistics.
de Saussure, F. (1931). Cours de Linguistique Generale. Payot, Paris.
Devlin, J., Chang, M.-W., Lee, K., und Toutanova, K. (2019). BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Burstein, J., Doran, C., und Solorio, T., Herausgeber, Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), Seiten 4171–4186, Minneapolis, Minnesota. Association for Computational Linguistics.
Goodfellow, I., Bengio, Y., und Courville, A. (2016). Deep Learning. MIT Press.
Goyal, A., Lamb, A. M., Zhang, Y., Zhang, S., Courville, A. C., und Bengio, Y. (2016). Professor Forcing: A New Algorithm for Training Recurrent Networks. In Lee, D., Sugiyama, M., Luxburg, U., Guyon, I., und Garnett, R., Herausgeber, Advances in Neural Information Processing Systems, Band 29. Curran Associates, Inc.
Hochreiter, S. und Schmidhuber, J. (1997). Long Short-Term Memory. Neural Comput., 9(8):1735–1780.
Radford, A., Narasimhan, K., Salimans, T., und Sutskever, I. (2018). Improving Language Understanding by Generative Pre-Training. Technical report, OpenAI.
Raschka, S., Liu, Y., und Mirjalili, V. (2022). Machine Learning with PyTorch and Scikit-Learn: Develop machine learning and deep learning models with Python. Packt Publishing.
Sutskever, I., Vinyals, O., und Le, Q. V. (2014). Sequence to sequence learning with neural networks. In Proceedings of the 27th International Conference on Neural Information Processing Systems - Volume 2, NIPS’14, Seite 3104–3112, Cambridge, MA, USA. MIT Press.
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L. u., und Polosukhin, I. (2017). Attention is All you Need. In Guyon, I., Luxburg, U. V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., und Garnett, R., Herausgeber, Advances in Neural Information Processing Systems, Band 30. Curran Associates, Inc.
Zellers, R., Bisk, Y., Schwartz, R., und Choi, Y. (2018). SWAG: A Large-Scale Adversarial Dataset for Grounded Commonsense Inference. In Riloff, E., Chiang, D., Hockenmaier, J., und Tsujii, J., Herausgeber, Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, Seiten 93–104, Brussels, Belgium. Association for Computational Linguistics.
Zhang, B., and Sennrich, R. (2019). Root mean square layer normalization. Proceedings of the 33rd International Conference on Neural Information Processing Systems. Curran Associates Inc., Red Hook, NY, USA.
Version 1.1
Enjoy Reading This Article?
Here are some more articles you might like to read next: